Algorytmy - teoria
Z pojęciem algorytmu wiąże się pojęcie złożoności obliczeniowej. Krótko mówiąc, złożoność określa jak dobrze wykonaliśmy jakieś zadanie. Każde zadanie można wykonać na wiele sposobów. Czasem aby uzyskać porządany efekt potrzebujemy dużo czasu angażując przy tym wiele zasobów (pamięci). Innym razem (inną metodą) możemy to samo uzyskać dużo szybcej przy wykorzystaniu mniejszej ilości pamięci. Ważne jest nie tylko by coś działało, ale też by działało możliwie optymalnie.
Złożoność obliczeniowa określa na ile dobrze udało nam się coś zrobić.
Istnieje wiele gotowych algorytmów, o różnej złożóności obliczniowej, które w efekcie dają to samo rozwiązanie. Poniżej znajdziecie listę niektórych z tych, które będziemy poznawać na zajęciach.
- NWW - algorytm wyznacza najmniejszą wspólną wielokrotność dwóch liczb
- NWD (algorytm Euklidesa) - algorytm wyznacza największy wspólny dzielnik dwóch liczb
- Sito Eratostenesa - algorytm wyszukujący liczby pierwsze z podanego zakresu (od 2 do n) bez wyznaczania liczby dzieliników
- Szyfr Cezara - szyfr przestawieniowy

- Szyfry podstawieniowe
- Kodowanie Huffmana - kompresja danych
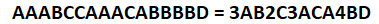
- Sortowanie bąbelkowe
- Sortowanie przez wybór
- Sortowanie przez wstawianie
- Algorytmy rekurencyjne
- Metoda Monte Carlo